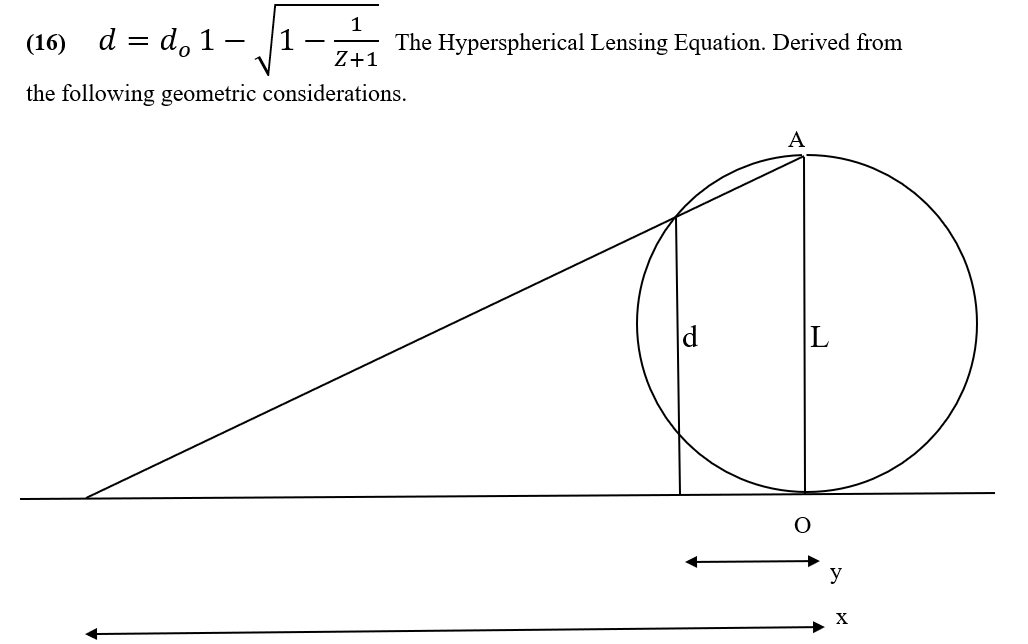

Equation 16
A stereographic projection can show the effect of projecting an n-sphere into an n-dimensional space.
For the purposes of Hypersphere Cosmology, we require a projection of a 3-sphere into three-dimensional space as observers will measure light as having travelled to them in ‘straight’ lines.
The diagram shown projects a 1-sphere (a circle) into a 1-space (a line), but this will suffice as we only need to know the distortion of distance.
Imagine first the projection of a 2-sphere (say a globe) into a 2-space (a flat surface). Imagine that we construct a wire frame globe with lines of latitude and longitude made of wires. If we place the globe south pole down on a sheet of paper and then place a lightbulb just inside the smallest ring of latitude around the north pole. The light will throw a shadow of the latitude wires of the globe onto the paper. The latitude rings close to the south pole will appear as circles close to the south pole on the paper, but latitude rings further from the south pole will start to appear exponentially larger and further away from the south pole on the paper. In principle, the shadow from latitudes very close to the north pole will go off the edges of a sheet of paper of any size.
Now a Glome-type hypersphere has the property that its circumference equals twice its antipode length L, so the distance d equals the distance around the circumference from the observer at the origin O at which we seek to determine the projection.
Such stereographic projections project a circle into an ever more widely spaced series of points on a line. A sphere becomes a series of ever more widely spaced concentric circles on a plane, a Glome hypersphere becomes an ever more widely spaced series of concentric 3D spheres. The equation shows the same distance relationship in all the various dimensional scenarios.
By expressing distance d over antipode length L and converting to redshift Z using the Redshift-Distance Equation we can relate the distance distortion from apparent to actual distance caused by lensing directly to redshift.
This shows that the universe does not undergo an accelerating expansion and does not need Dark Energy. It also allows a precise determination of the antipode length of the universe by Equation 17.